Sisältö

• Askeleet
• vinkkejä

Matemaatikkojen ja grafiikkaohjelmoijien on usein löydettävä kulma kahden vektorin välillä. Onneksi tämän kulman laskemiseen käytetty kaava ei edellytä muuta kuin yksinkertaista skalaarituotetta. Vaikka tämän kaavan perusteet on helpompi ymmärtää käytettäessä kaksiulotteisia vektoreita, voimme helposti mukauttaa sen vektoreihin, joissa on mikä tahansa lukumäärä komponentteja.

Askeleet

Osa 1/2: Laske kulma kahden vektorin välillä

1. 

   Tunnista kaksi vektoria. Kirjoita kaikki tunnetut tiedot kahdesta vektorista. Tämän oppaan tarkoituksia varten oletamme, että tunnet vektorit vain niiden mittakoordinaattien suhteen (kutsutaan myös komponentit). Jos tiedät jo moduuli tai standardi näistä vektoreista (ts. niiden pituus), voit ohittaa jotkut alla olevista vaiheista.
   • Esimerkki: Tarkastellaan kaksiulotteisia vektoreita = (2,2) ja = (0,3). Nämä kaksi vektoria voidaan kirjoittaa uudelleen = 2minä + 2j e = 0minä + 3j = 3j.
   • Vaikka esimerkissämme käytetään kahta kaksiulotteista vektoria, voimme soveltaa seuraavia ohjeita vektoreihin, joissa on mikä tahansa lukumäärä komponentteja.

2. 

   
   
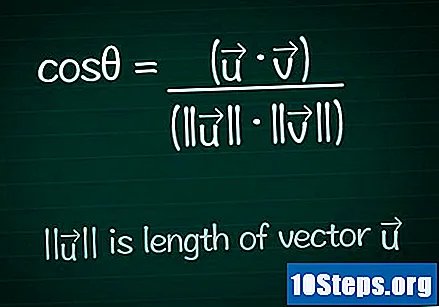
   Kirjoita kosinuskaava. Kaikkien kahden vektorin välisen kulman any arvon löytämiseksi meidän on ensin laskettava kyseisen kulman kosinus. Voit etsiä ja selvittää kaavan yksityiskohtaisesti tai kirjoittaa sen sellaisena kuin se on alla:
   • cosθ = (•) / (|||| ||||)
   • |||| edustaa moduuli (tai vektorin pituus) ".
   • • edustaa skalaarituote (tai sisäinen tuote) kahdesta vektorista.

3. 

   
   
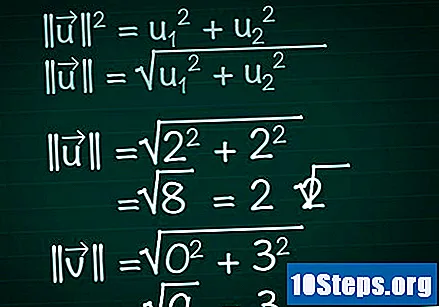
   Laske kunkin vektorin moduuli. Kuvittele komponentin muodostama suorakulmainen kolmio x vektorista, sen komponentista y ja itse vektori. Tässä kolmiossa vektorilla on hypoteenuksen rooli; Siksi sen pituuden löytämiseksi käytämme Pythagoraan lausetta. Seurauksena on, että tätä kaavaa voidaan helposti soveltaa vektoreihin, joissa on mikä tahansa lukumäärä komponentteja.
   • || u || = u₁ + u₂. Jos vektorissa on enemmän kuin kaksi komponenttia, jatka vain + u: n lisäämistä₃ + u₄ +...
   • Siksi kaksiulotteisen vektorin tapauksessa meidän on || u || = √ (u₁ + u₂).
   • Esimerkissämme |||| = √ (2 + 2) = √ (8) = 2√2. |||| = √(0 + 3) = √(9) = 3.

4. 

   
   
   Laske skalaarituote kahden vektorin välillä. Sinun pitäisi jo tietää vektoreiden kertomistapa, jota kutsutaan myös skalaarituote. Laskeaksesi kahden vektorin skalaarituotteen niiden komponenttien perusteella kerrotaan komponentit samaan suuntaan toistensa kanssa ja lisäämme sitten näiden tuotteiden tulokset.
   • Jos työskentelet tietokonegrafiikkaohjelmien kanssa, käy ensin "Vinkit" -osiossa ennen kuin jatkat.
   • Matemaattisesti • = u₁v₁ + u₂v₂, missä u = (u₁, u₂). Jos vektorissasi on enemmän kuin kaksi komponenttia, jatka vain + u: n lisäämistä₃v₃ + u₄v₄...
   • Esimerkissämme = = u₁v₁ + u₂v₂ = (2)(0) + (2)(3) = 0 + 6 = 6. Tämä on vektorien ja.

5. 

   Korvaa nämä tulokset kosinuskaavassa. Muista, cosθ = (•) / (|||| || ||). Olemme jo laskeneet kahden vektorin skalaarituotteen ja moduulin. Korvataan nyt nämä arvot kaavassa ja lasketaan kulman kosini.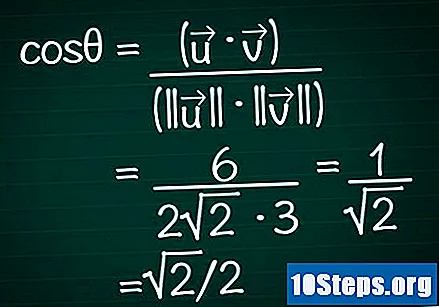
   • Esimerkissämme cosθ = 6 / (2√2 * 3) = 1 / √2 = √2 / 2.

6. 

   Löydä kulma kosinussi perusteella.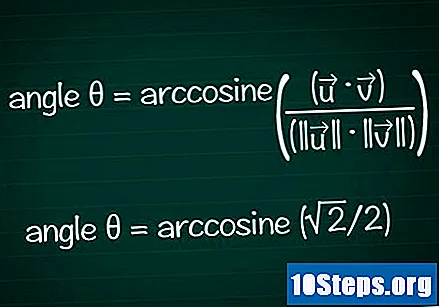
   Käytä laskimen kaari- tai cos-toimintoa kulman determine määrittämiseksi kosinin arvosta. Joissain tapauksissa saatat pystyä löytämään kulma-arvon yksikköympyrän perusteella.
   • Esimerkissämme cosθ = √2 / 2. Kirjoita laskimeesi "arccos (√2 ​​/ 2)" löytääksesi kulman. Toinen vaihtoehto on etsiä yksikköympyrän kulma θ, missä cosθ = √2 / 2: tämä pätee θ = /₄ tai 45 °.
   • Kun kaikki tiedot kootaan, meillä on lopullinen kaava θ = arkkosiini ((•) / (|||| || ||))

Osa 2/2: Kaavan määrittäminen kulman laskemiseksi

1. 

   Ymmärrä kaavan tarkoitus. Kaavaa, jota lasimme kahden vektorin välisen kulman laskemiseksi, ei johdettu jo olemassa olevista säännöistä; sen sijaan se luotiin määritelmäksi kahden vektorin välinen skalaarituote ja niiden välinen kulma. Tämä päätös ei kuitenkaan ole mielivaltainen. Kun tarkastelemme lähemmin perusgeometriaa, voimme nähdä, miksi tämä kaava johtaa sellaisiin hyödyllisiin ja intuitiivisiin määritelmiin.
   • Seuraavat esimerkit hyödyntävät kaksiulotteisia vektoreita, koska ne ovat intuitiivisimpia tyyppejä työskennellä. Kolmen tai useamman ulottuvuuden vektorien ominaisuudet määritetään yleisestä kaavasta (myös hyvin samanlaisella tavalla).

2. 

   Tarkista kosinuslaki. Tarkastellaan missä tahansa kolmiossa kulmien θ muodostamia puolia ja B ja sivu ç vastapäätä sitä kulmaa. Kosinuslain mukaan c = a + b -2abvyötärönauha(Θ). Tämän kaavan osoittaminen voidaan saada helposti geometrian perusteista.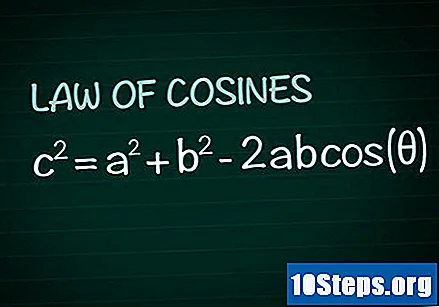

3. 

   Yhdistä kaksi vektoria muodostamaan kolmio. Piirrä pari vektoria ja niiden väliin kulmalla angle. Piirrä sitten kolmas vektori niiden väliin muodostamaan kolmio. Toisin sanoen piirrä vektori siten, että + = tai yksinkertaisesti = -.

4. 

   Sovita kosinuslaki tähän kolmioon. Korvaa sivumme pituus vektori kolmio (eli vektorimoduuli) kosinuslain kaavassa:
   • || (a - b) || = || a || + || b || - 2 || a || || b ||vyötärönauha(θ)

5. 

   Kirjoita kaava uudelleen skalaarituotteilla. Muista, että pistetuote on toisen vektorin suurennus. Itse vektorin skalaarituote ei vaadi projisointia, koska suunnassa ei ole muutoksia. Tämä tarkoittaa, että • = || a ||. Kirjoittakaamme näiden tietojen perusteella kosinin lain yhtälö:
   • (-) • (-) = • + • - 2 || a || || b ||vyötärönauha(θ)

6. 

   Yksinkertaista kaavaa. Laajenna yhtälön vasemmalla puolella olevia tuotteita ja yksinkertaista sitten, kunnes saavutat kaavan, jonka tiedämme kulmien laskemiseksi.
   • • - • - • + • = • + • - 2 || a || || b ||vyötärönauha(θ)
   • - • - • = -2 || a || || b ||vyötärönauha(θ)
   • -2 (•) = -2 || a || || b ||vyötärönauha(θ)
   • • = || a || || b ||vyötärönauha(θ)

vinkkejä

• Nopeaa resoluutiota varten käytä seuraavaa kaavaa mihin tahansa kaksiulotteiseen vektoripariin: cosθ = (u₁ • v₁ + u₂ • v₂) / (√ (u₁ • u₂) • √ (v₁ • v₂)).
• Jos työskentelet tietokonegrafiikkaohjelmien kanssa, sinun on todennäköisesti tiedettävä vain vektorien suunta, ei niiden pituus. Seuraa alla olevia vaiheita yhtälöiden yksinkertaistamiseksi ja ohjelman nopeuttamiseksi:
  • Normalisoi kukin vektori, ts. Löydä yksikkövektori, jolla on sama suunta kuin alkuperäisellä vektorilla. Voit tehdä tämän jakamalla vektorin jokainen komponentti vektorimoduulilla.
  • Laske normalisoitujen vektorien skalaarituote, ei alkuperäiset vektorit.
  • Koska normalisoitujen vektorien moduuli (ts. Pituus) on yhtenäinen, voimme jättää ne kaavan ulkopuolelle. Lopullinen yhtälö kulmien laskemiseen on kaaria (•).
• Kosinuslain kaavan perusteella voimme nopeasti selvittää, onko kyseinen kulma akuutti vai tylppä. Aloita cosθ = (•) / (|||| ||||):
  • Yhtälön vasemmalla ja oikealla puolella on oltava sama merkki (positiivinen tai negatiivinen).
  • Koska pituudet ovat aina positiivisia, cosθ: lla on aina sama merkki kuin skalaarituotteella.
  • Siksi, jos skalaarituote on positiivinen, cosθ on positiivinen. Tämä tarkoittaa, että kulma on yksikköympyrän ensimmäisessä kvadrantissa, ts. Θ <π / 2 tai 90 °. Siksi kulma on akuutti.
  • Jos skalaarituote on negatiivinen, cosθ on negatiivinen. Tämä tarkoittaa, että kulma on yksikköympyrän toisessa kvadrantissa, ts. Π / 2 <θ ≤ π tai 90 ° <θ ≤ 180 °. Siksi kulma on tylppä.